-
- Identities inspired
from Ramanujan Notebooks II
- by Simon Plouffe, July
21, 1998
-
-
- These identities where found using an
implementation of LLL algorithm in Pari-Gp (2.0.10) +
MapleV.5
- see also these other identities found in 1993
about Catalan.
They are not knew, the presentation is.
-
-
-
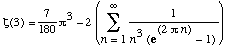



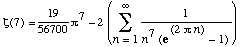
-
-
- They are all inspired by Ramanujan formulas in
Bruce Berndt's book (Ramanujan Notebooks II, chapter 14
formulas 25.1 and 25.3. Formula 25.1 is

-
- This sum suggests that (by splitting the sum)
there could be one with Zeta(3), which is the case. The
coefficients are the same. Formula 25.2 confirm that observation.
Formula 25.3 gives a clue on a general formula as well with
Bernoulli numbers.
-
- NOTE
:The formulas for Zeta(4*n+3) appeared in
"On the Khintchine Constant" by Bailey, Borwein and Crandall, Math
of Computation, 66 #217, page 413 (1997). There is one for
Zeta(4*n+1) but that one on Zeta(5) is simpler.
-
- I could compute 39000 digits of Zeta(5)
and 50000 digits of Zeta(7) with it. The convergence rate
is rather good since 1/exp(2*Pi) = 1/535.49, it gives 2.72 digits/
term. Those formulas can probably be programmed to get 1 million
digits of Zeta(2*n+1), Zeta(3) is already known to 32 million
digits.
-
- The computation is rather straightforward
since we already have Pi to many billion of digits, the harder
part is the evaluation of exp(2*Pi) but it can be done only
once.
-
- See also these new
ones in the same vein (August 7,
1998).
-
- Here are the other identities found with
Zeta(9) to Zeta(21) and the results of Joerg
Arndt as computed on July 27 up to
Zeta(163).
/infinity \
| ----- |
| \ 1 |
37122624 | ) --------------------|
| / 9 |
| ----- n (exp(2 Pi n) - 1)|
\ n = 1 /
/infinity \
| ----- |
| \ 1 | 9
+ 74844 | ) --------------------| + 18523890 Zeta(9) - 625 Pi = 0
| / 9 |
| ----- n (exp(2 Pi n) + 1)|
\ n = 1 /
/infinity \
| ----- |
| \ 1 | 11
-851350500 | ) ---------------------| - 425675250 Zeta(11) + 1453 Pi = 0
| / 11 |
| ----- n (exp(2 Pi n) - 1)|
\ n = 1 /
/infinity \
| ----- |
| \ 1 |
514926720 | ) ---------------------|
| / 13 |
| ----- n (exp(2 Pi n) - 1)|
\ n = 1 /
/infinity \
| ----- |
| \ 1 | 13
+ 62370 | ) ---------------------| + 257432175 Zeta(13) - 89 Pi = 0
| / 13 |
| ----- n (exp(2 Pi n) + 1)|
\ n = 1 /
/infinity \
| ----- |
| \ 1 |
-781539759000 | ) ---------------------| - 390769879500 Zeta(15)
| / 15 |
| ----- n (exp(2 Pi n) - 1)|
\ n = 1 /
15
+ 13687 Pi = 0
/infinity \
| ----- |
| \ 1 |
3808863131673600 | ) ---------------------|
| / 17 |
| ----- n (exp(2 Pi n) - 1)|
\ n = 1 /
/infinity \
| ----- |
| \ 1 |
+ 29116187100 | ) ---------------------|
| / 17 |
| ----- n (exp(2 Pi n) + 1)|
\ n = 1 /
17
+ 1904417007743250 Zeta(17) - 6758333 Pi = 0
/infinity \
| ----- |
| \ 1 |
-42877225028137500 | ) ---------------------|
| / 19 |
| ----- n (exp(2 Pi n) - 1)|
\ n = 1 /
19
- 21438612514068750 Zeta(19) + 7708537 Pi = 0
/infinity \
| ----- |
| \ 1 |
-3762129424572110592000 | ) ---------------------|
| / 21 |
| ----- n (exp(2 Pi n) - 1)|
\ n = 1 /
/infinity \
| ----- |
| \ 1 |
- 1793047592085750 | ) ---------------------|
| / 21 |
| ----- n (exp(2 Pi n) + 1)|
\ n = 1 /
21
- 1881063815762259253125 Zeta(21) + 68529640373 Pi = 0